8月の中学生クラスでは、結び目の数学をやっています。
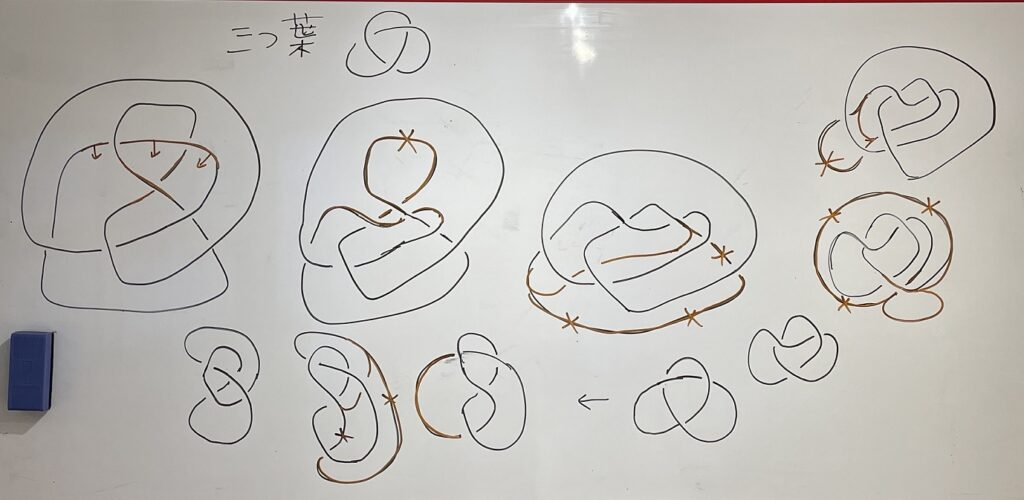
結び目の数学では、紐の結び方を研究します。結び目にはいろいろな結び方(堅結び、蝶結びなど)がありますが、見かけ上は複雑でも解ける結び目かどうかを判断したり、異なる結び目が本当に異なるのかどうかを判定することが基本となります。
数字が書けないと、計算ができないのと同じように、結び目を研究するには結び目を紙の上に描けなければいけないことに気付きます。毛糸や紐で結び目を作り、それを手で操っていろいろな形に変形してみるという実験ももちろん大切なのですが、毛糸を使うとしても、それで分かったことを紙に書いておかなければ、次への発展がありません。しかし、やってみると分かるのですが、結び目を紙に書くのはなかなか大変です。これには慣れが必要でしょう。1週間ぐらいの間、毎日少しずつ練習すると、かなり思った通りの図が描けるようになりますが、それにしてもなかなかうまくはいかないものです。もちろん、結び目を見た目がきれいに、つまり、エレガントにとか、お洒落にとか、言い方はいろいろありますが、描けることと数学とは関係がありません。図が下手でも数学はできます。それよりも問題なのは、自分が描いた図であっても、一晩寝て、次の日に眺めてみると、いったい何の図だったのかわからなくなってしまうことです。いちおう、これは「三つ葉結び目の新種発見か?」などの注釈を図の横に書き添えておくのですが、それでも少し時間が経つと、あれ、この図はなにをやっていたんだっけ?という状態になってしまいます。
もうひとつ、重要なことは、手で図を描く練習をしながら、同時に頭の中で結び目を動かすことが少しずつできるようになっているということです。つまり、空間配置を認識するコツを掴むというか、そういうふうなことです。
結び目の図を見ただけで、ああ、これは○○の結び目だとわかるようになるというのは、おそらく自転車に乗れるようになるのと似て、難なくできるようになってみると、どうしてそんなことで苦労していたのか、自分ながらわからないという状態になるものなのでしょう。
数学を勉強していくと、4次元の図形を頭の中で操作したり、変形したり、あっちから見て考えたり、こっちから見て考えたりといったことが、何とかできなければいけないといった場面に遭遇します。でも、それは簡単には絵に描けないこともあって、なかなか難しい作業です。そうなると、もうエレガントな図にしなくちゃなんてことは、言っていられなくなってきます。何しろ、図に頼ることもできず、先生や先輩の話もチンプンカンプンで、自分の頭の中に4次元空間を創造するほかはないのです。
