8月18日、19日の小学校1-2年生クラスでは、円の焦線を描きました。
円周を等分割する点(たとえば、24等分点)をとり、0から順に番号を振ります。
次に、1番から2番、2番から4番、3番から6番というふうに各点に対してその番号が2倍になっている点を見つけて結んでいくと、円の焦線が描けます。
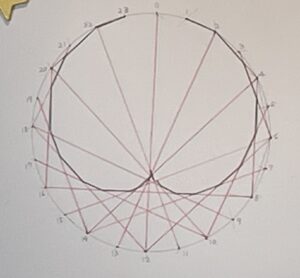
円の焦線の作図
円の焦線は日常の生活の中でも見つけることができます。下の写真はわたしが好きなアフターヌーンティーのチャイです。チャイの水面に照明の平行光線が当たると円形の茶碗で反射した反射光が集まって明るく光る曲線が現れます。これが焦線です。

ティーカップの水面に映る円の焦線
なお、このような図形を描くとき、点には大きさがないことに注意する必要があります。「点」の概念については、多くの子どもは点を丸いものとしてイメージしているという研究結果があります(ジョージ・レイコフ他『数学の認知科学』丸善出版)。一方、数学における点は大きさがゼロであり、直線には幅がありません。ユークリッドは「点とは大きさのない位置である」そして「線とは幅のない長さである」と書いています(ユークリッド『原論』紀元前300年ごろ成立)。点を描きなさいというと大きな黒丸を描く子どもがいますが、そうすると正確な作図はできず、描いた図形の美しさも損なわれます。かといって、点にまったく大きさがなければ見えませんから作図することもできないわけです。小学生には、大きさのない点、幅のない線をイメージしながら、なるべく小さな点を打ち、線はなるべく細く描くように明示的に指導しましょう。
円の焦線は、レンズ設計に応用されています。たとえば、乱視用の眼鏡に使うレンズを設計するとき、焦線の計算は必須です。
点と点の結び方の規則を少し変えると、今度は下図のような尖(とん)がりが2つある包絡線を描くこともできます。数では円周を48等分する点を使っていますが、各点について番号が3倍となる点を結べばできます。
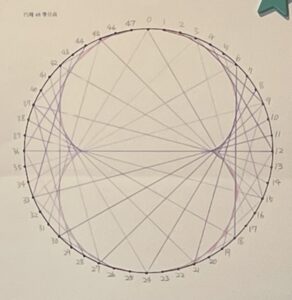
番号を3倍した点を結んでできる曲線
かけ算は小学校では2年生で習いますが、1年生でも同じ数を3つ足し算することで計算できます。簡単な計算できれいな図形が描けることは体験してみなければわかりません。算数の専門書には算数の内容が計算の分野、図形の分野などにわかれるように書かれていますが、互いに関連させながら教えることで楽しく興味をもって勉強することができるでしょう。
—授業のようすはインスタグラムでも見ることができます。随時更新していますので、ご覧ください。
