8月12日の小1-2年クラスでは、円の中に包絡線を描きました。
円周を等分する点を取り、それらを適当に結んでいくと、包絡線が見えてくることがあります。今回は、円周をn等分する点を頂点とする正n角形の対角線のうちで、同じ長さの対角線を結んでいきました。
たとえば、円周を24等分する24個の点をとり、0から23までの番号を振ります。次に、0と4、1と5というふうに、差が4になる点どうしをすべて結ぶと、円周に近いところにひとまわり小さな円が包絡線として描けます。この「円」は正確には「折れ線」つまり、線分の集合なのですが、遠目に見ると円に見えます。今回の包絡線は円です。
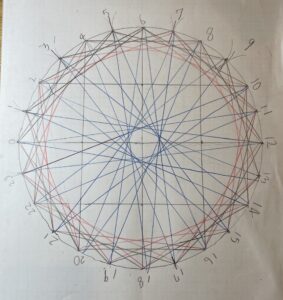
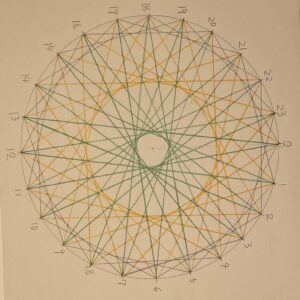
包絡線はとる点の個数を順次増やしていくとだんだんと細かくなり、ついには曲線に近づいていくという性質があります。この曲線が包絡線なのです。
包絡線にはまた、直線群が通過する領域と通過しない領域との間の境界線であるという性質もあります。
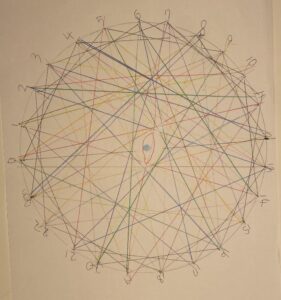
つぎに、たとえば番号の差が8となる点をすべて結んだり、番号の差が22となる点をすべて結んだりすると、もう少し小振りの円が現れてきたり、中心の近くに小さく固まった円が描けたりします。
直線は定規で描きましたが、等分点をより多くとり、直線をより正確に引くとだんだんと真円に近づいていくようすがわかるでしょう。
対角線を引いていくと、はじめは星形のような形が見えてきますが、だんだんと直線を増やしていくと、真ん中の付近にぽっかり白い領域が残るのがわかるでしょう。
ちょうどお盆でお休みの時期だったので、お父さまの帰省先のフランスからZoomで授業に参加したお友だちもいました。授業中に時間を確かめると、そのとき日本時間では18:10でしたが、フランスでは11:10でした。
今回は、直線を引きながら足し算の練習もしたことになります。次回をお楽しみに。
—授業のようすはインスタグラムでも見ることができます。随時更新していますので、ご覧ください。
