8月13日の小学校5-6年クラスでは、オイラーの多面体定理を勉強しました。
始めに正多面体の定義の3つの条件を復習したあと、実際にポリドロンで5種類の正多面体を作ってみました。そして、頂点、辺(稜)、面の個数を数えてみると、表のようになりました。
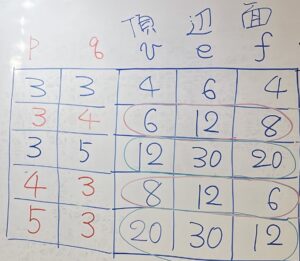
この表には面白い性質がいろいろあります。表の数字を見てすぐに気がつくものもあれば、なかなか気づきにくい性質もあります。気づきにくい性質のひとつは、頂点、辺、面の個数を v, e, f とすると、
v – e + f = 2
となるという性質で、この性質は任意の凸多面体について成り立ち、オイラーの多面体定理またはオイラーの多面体公式と呼ばれています。この公式は凸多面体だけでなく、一般に穴の開いていない閉じた多面体であればいつでも成り立ちます。
この数 2 を多面体のオイラー数といいますが、一般に穴が g 個開いている多面体のオイラー数をχ(カイ、ギリシャ文字の小文字)とすると、χ = 2 – 2 × g となることも知られています。
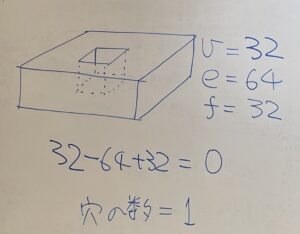
ためしに、穴が1個開いている多面体の例を正方形のポリドロンだけで作ってみると写真のようになりました。この多面体は頂点が32個、辺が64本、面が32面あるので、オイラー数は
32-64+32 = 0
となります。

また、セパタクローの競技用ボールの形を多面体とみなしたとき、頂点、辺、面の個数を数えると、オイラー数は2になることを計算で確かめました。写真はこの形をポリドロンで作ったものです。

—授業のようすはインスタグラムでも見ることができます。随時更新していますので、ご覧ください。
